第13天的编程挑战相对简单,尤其对数学基础扎实的朋友来说。起初我尝试蛮力法,但很快意识到随着难度增加,这种方法效率低下。在尝试解决这个问题时,我已经落后几天了。在参考了朋友的建议后,我研究了克莱默法则,最终找到了解决方案。

这是一个代码难题,涉及到一个非传统的爪机控制。我们有两个按钮,分别标记为a和b,它们控制爪机的移动方向,并且每个按钮的按下成本不同。
只要运用正确的数学方法,这个难题并不难。我们从解析输入数据开始:
cost_a = 3 cost_b = 1 type point = tuple[int, int] type vector = tuple[int, int] def extract_vector(input: str) -> vector: return tuple(int(item.strip().lstrip("x").lstrip("y")) for item in input.split(",")) def extract_point(input: str) -> point: return tuple(int(item.strip().lstrip("x=").lstrip("y=")) for item in input.split(",")) def parse(input: str, cost_a: int = cost_a, cost_b: int = cost_b) -> tuple[tuple[dict[vector, int], point], ...]: result = () button, goal = {}, () for line in input.strip().splitlines(): if line.startswith("button a:"): button[extract_vector(line.partition(":")[-1])] = cost_a elif line.startswith("button b:"): button[extract_vector(line.partition(":")[-1])] = cost_b elif line.startswith("prize:"): goal = extract_point(line.partition(":")[-1]) else: result += ((button, goal),) button, goal = {}, () return result + ((button, goal),)
我最近开始在我的代码中添加类型提示。虽然这不会提高运行时性能,但它极大地提高了代码的可读性,尤其是在使用支持良好类型提示的编辑器时。反复输入诸如tuple[int, int]之类的复杂类型很繁琐。幸运的是,Python 3.12引入了类型别名的功能,例如:
type point = tuple[int, int] type vector = tuple[int, int]
这显著提高了解析函数的可读性。解析函数返回一个元组,每个内部元组包含一个按钮成本映射和目标点。
克莱默法则非常适合解决二元一次方程组,这正是我们需要的。我们有两个方程,分别代表爪机在x和y方向上的移动:

其中:
- a_1, a_2: 按下按钮a引起的x和y方向移动
- b_1, b_2: 按下按钮b引起的x和y方向移动
- c_1, c_2: 奖品的目标x和y坐标
- x: 按下按钮a的次数
- y: 按下按钮b的次数
示例输入中,按钮a按了80次,按钮b按了40次。我们可以用这些数据验证线性方程。计算得到的x和y坐标验证了我们的方程。
现在我们已经验证了问题可以用线性方程表示,我们可以将其改写成适合应用克莱默法则的形式,从而求解按下每个按钮的次数。这需要将方程表示成矩阵形式,Ax = b:
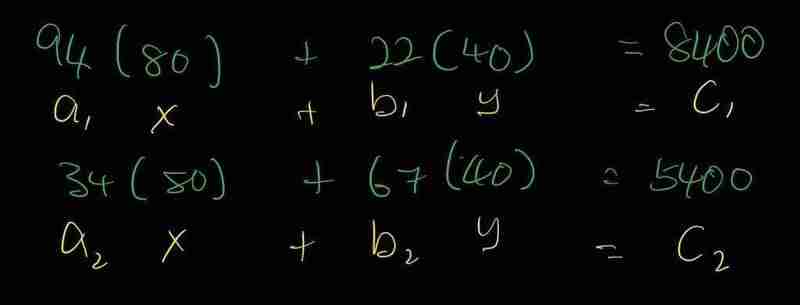
其中:
- A是系数矩阵
- x是包含按下每个按钮次数(x和y)的列矩阵
- b是包含目标x和y坐标的列矩阵
为了应用克莱默法则,我们首先需要计算矩阵A的行列式,记为d:

然后,我们计算行列式d_x和d_y。为了计算d_x,我们将常数矩阵b替换矩阵A的第一列。同样,为了计算d_y,我们将常数矩阵b替换矩阵A的第二列:

现在我们可以用克莱默法则计算按下按钮a (x) 和b (y) 的次数:
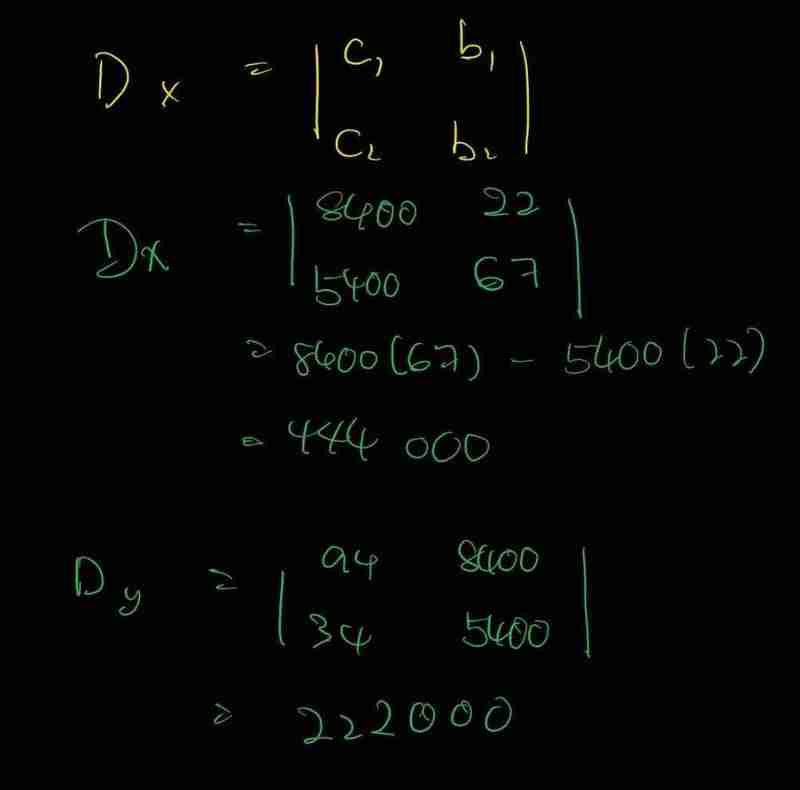
在实现中,我们需要一个函数来计算2×2矩阵的行列式。我们将矩阵表示为字典,键是(行,列)索引(从(0,0)开始),值是对应的矩阵元素:
def determinant(matrix: dict[point, int]) -> int: return matrix[(0, 0)] * matrix[(1, 1)] - matrix[(0, 1)] * matrix[(1, 0)]
接下来,我们实现使用克莱默法则解决难题的核心逻辑。find函数接收按钮移动和目标坐标作为输入,并返回每个按钮需要按下的次数:
def find(buttons: dict[vector, int], goal: point) -> dict[tuple[int, int], int]: button_a, button_b = tuple(buttons.keys()) result = {button_a: 0, button_b: 0} d = determinant( { (0, 0): button_a[0], (1, 0): button_a[1], (0, 1): button_b[0], (1, 1): button_b[1], } ) dx = determinant( { (0, 0): goal[0], (1, 0): goal[1], (0, 1): button_b[0], (1, 1): button_b[1], } ) dy = determinant( { (0, 0): button_a[0], (1, 0): button_a[1], (0, 1): goal[0], (1, 1): goal[1], } ) if dx % d == 0 and dy % d == 0: result = {button_a: dx // d, button_b: dy // d} return result
最后,我们组装第一部分的解决方案,它计算在所有爪机配置中获胜的总成本(点数)。它解析输入,使用find函数确定每个配置的按钮按下次数,并对按钮成本和按下次数的乘积求和:
def part1(input: str) -> int: return sum( buttons[button] * count for buttons, goal in parse(input) for button, count in find(buttons, goal).items() )
第二部分将1013添加到所需的x和y坐标。由于我们使用的是克莱默法则,只需简单地修改传递给find函数的目标坐标即可:
def part2(input: str) -> int: return sum( buttons[button] * count for buttons, goal in parse(input) for button, count in find( buttons, tuple(item + 10000000000000 for item in goal) ).items() )
这个难题比后来的代码挑战简单,但编写这篇文章却花费了更多时间。我必须仔细检查公式以确保准确性,并经常参考我的笔记以避免错误。我花在写这篇文章上的时间肯定比解决难题本身更多。
这就是本周的编程挑战。如果您正在寻找软件工程师加入您的团队,请随时联系!感谢您的阅读,我们下周再见!
以上就是在代码出现第13天应用Cramer的规则的详细内容,更多请关注php中文网其它相关文章!
 微信扫一扫打赏
微信扫一扫打赏
 支付宝扫一扫打赏
支付宝扫一扫打赏

