深入浅出神经网络：理解微积分的精髓

大家好，我是Hexmos的创始人Shrijith Venkatrama。我目前正在开发LiveaPi，一个简化API文档生成的。

神经网络看起来复杂，但其核心思想却出奇地简单：导数。Andrej Karpathy的Micrograd项目完美诠释了这一点——仅用不到150行Python代码，就清晰地展现了神经网络的基本原理。本文将循序渐进地讲解Micrograd，从最基础的概念开始，逐步深入。您将学习：

• 导数的真正含义及其计算方法
• 符号微分与数值微分之间的
• 微小输入变化如何影响输出（正、负和零斜率）
• 神经网络不需要显式导数公式

我们将通过图解、简短代码示例和实用见解，帮助您理解梯度下降如何驱动神经网络学习，避免不必要的复杂性。让我们开始吧！

Karpathy的Micrograd项目仅包含两个文件：

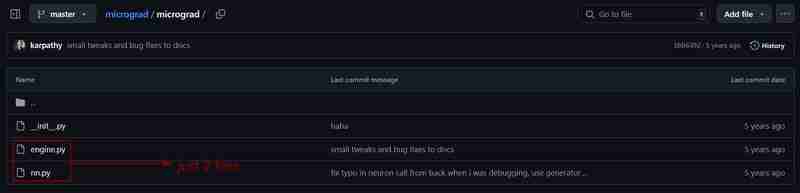
• Engine.py：不到100行代码，定义了值类，是神经网络运行的核心。
• nn.py：定义了神经元、层和多层感知器（MLP），约60行代码。

核心思想：不到150行简洁的Python代码，就足以捕捉神经网络的核心思想。其他库中代码的复杂性主要在于效率的提升。

理解导数：基础概念

首先，让我们通过几个例子来理解导数的概念：

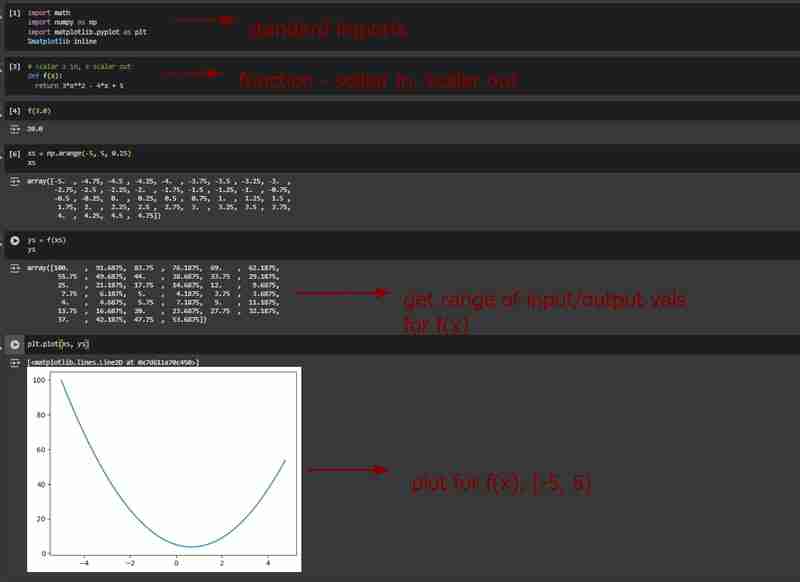
1. 定义一个函数f，接收标量输入，返回标量输出。
2. 生成一系列x值（输入）和对应的y值（输出）。
3. 绘制函数图像。
4. 计算导数的两种方法：

我们的目标是在特定点（例如x=3）找到函数的导数。在学校，我们通常学习的是符号微分法。

例如，对于表达式3*x*2 – 4x + 5，我们可以求出导数表达式为6*x – 4。然而，在神经网络中，我们处理的表达式可能非常复杂，不可能手动求导。

因此，我们采用数值微分法。但在学习数值微分之前，先理解导数的概念非常重要。

可微函数的含义

关键公式如下：

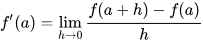
公式中，h是一个很小的值，并且趋近于0。我们关注的是：当输入发生微小变化时，函数输出的趋势是什么？更具体地说，在x点，如果我们增加一个微小的量h，输出会增加还是减少？变化的大小是多少？

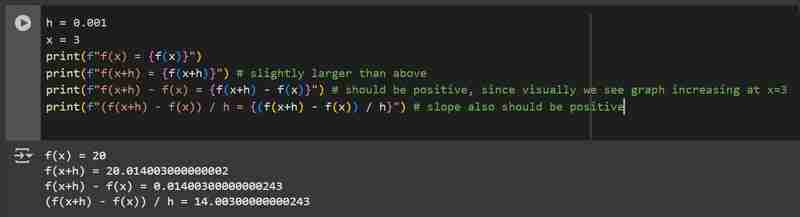
公式的结果代表斜率。如果输入的微小增加导致正斜率，则输出值增加；如果导致负斜率，则输出值减少。

在某些点上，输入的微小增加可能不会改变输出，此时斜率为零。

数值实验

我们可以通过数值实验来验证上述直觉，使用一系列有效的x值和一个微小的h值。

• 正斜率示例
• 负斜率示例
• 零斜率示例

参考：神经网络和反向传播的简明介绍：构建Micrograd

以上就是用微衍生物从头开始了解反向传播的详细内容，更多请关注php中文网其它相关文章！